Analyzing what happens where interfaces meet and mix is essential toward understanding and controlling fundamental mechanisms in both natural and industrial systems. By considering the reaction front of heterogeneous fluid flows in porous media, whose reaction rates are sharply influenced by compression and diffusion, researchers from Massachusetts Institute of Technology, Spanish National Research Council, Université de Rennes 1 (France), and Pacific Northwest National Laboratory developed a new model for predicting reaction front kinetics in these flows that provides a more complete assessment regarding the effects of many processes—stretching, coalescence, and fluid particle dispersion—on reactive transport dynamics.
Understanding the dynamics of mixing on reaction kinetics at the pore scale can directly influence the quality and usability of models used to measure reactive transport in carbon dioxide storage, subsurface flow and transport (contaminant transport/reactivity in hydrological systems), or mixing-driven biochemical processes in filters and/or living tissues. Each of these areas has distinct relevance to current U.S. Department of Energy mission objectives.
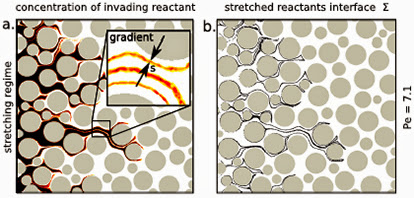
As fluids traverse the porous media, they form thin, membrane-like structures, or lamellae, that ultimately coalesce. These lamella-like structures evolve due to compression, diffusion, and merging, which governs the temporal evolution of the global reaction rates. In their work, the researchers considered two reactants (A and B) mixed to form a product C, according to the irreversible reaction A + B → C, in a solution flowing through a porous medium whose heterogeneity determined the front geometry. They used the smoothed particle hydrodynamics (SPH) method to solve the governing Navier-Stokes and advection-diffusion-reaction equations.
In their four simulations (Péclet number values, Pe = 0.071, 0.71, 2.4, and 7.1), they saw how flow affected mixing. In the “stretching regime,” the interface between the reactants organized into complex, elongated lamellae. As the reactant lamellae began to coalesce by diffusion, the process became less linear, and the interface width decreased due to compression induced by the flow stretching. Meanwhile, during the “coalescence regime,” the front topology changed, forming an aggregate of lamellae bundles. The researchers determined that the number of bundles in a pore is inversely proportional to the interface width, which limits the available space for them to coexist. As width increased, the bundles continued to merge, decreasing their numbers. This happens because the local diffusive growth contributes to bundle coalescence—but not to growth of the mixing area. Thus, the dominant effect for mixing in this regime is fluid advection.
The generated model accounted for the competition between compression and diffusion in the evolving concentration gradients, as well as the dynamics of the lamella merging in a unique formulation.
“The proposed model is applicable for various reactive systems, not just for flow in porous media. In most natural and engineered reactive systems, the large-scale behavior depends closely on the mixing and reactions occurring at the microscale,” explained Dr. Alexandre Tartakovsky, associate division director for computational mathematics at PNNL and a co-author of the paper.
“This new method provides a more complete look at the reaction front kinetics—one that accounts for compression, diffusion, and lamellae behaviors—rather than being based solely on geometric analysis,” he added. “It has great potential for improving reactive transport modeling used in a range of applications.”
While this novel simulation elucidates the role of chemical reaction dynamics in heterogeneous mixing fronts and offers new perspectives for upscaling reaction kinetics in heterogeneous flows through porous media, the model has potential for wider applicability to other heterogeneous flow analyses.
Reference:
de Anna P, M Dentz, A Tartakovsky, and T Le Borgne. 2014. “The filamentary structure of mixing fronts and its control on reaction kinetics in porous media flows.” Geophysical Research Letters 41(13):4586-4593. DOI: 10.1002/2014GL060068.
Note : The above story is based on materials provided by Pacific Northwest National Laboratory.










